Basic Shadow projection

Introduction

Well this is basically just another document on how to create projected shadows, but I will show you how the matrix used to create the shadow projection is correctly derived instead of just showing how it works. So if you follow carefully my calculations you will completely understand why this really works :)

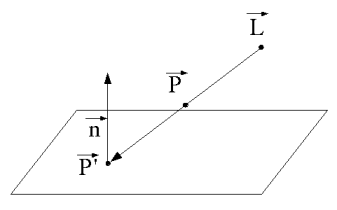
First have a look at the scenario we are going to use: In the following image you see a ray of light that starts at the light-source L, goes through a point of the shadow-throwing object P finally reaching its destination in the point P' on the ground plane. The vector n is the normal vector of the plane.

Figure 1: The scenario of the shadow projection

This approach might seem a bit "strange" as we want to create a shadow and not draw all vertives on the ground, but thats exactly what we need to do. A shadow is mathematically spoken just a projection of an object onto a plane seen from a light source.

Because nearly every projection can be represented using a matrix, we will now derive a matrix that does exactly this projection for us. We want a matrix that turns every object we draw into a shadow of itself.

We assume the following:

Let L be the position of the light
P the position of a vertex of the object we want to shadow
E a point of the plane (not seen in the figure)
n the normal vector of the plane

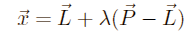
The straight that goes from the light source through our point is:

(this is just the standard line-formula)

The plane that our shadow will be projected on is:

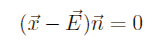
(this is the Euler-form of a plane as far is remember the name)

Now we insert the straight formula into the plane formula:

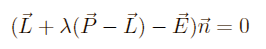
(so we get the point where the light ray and the plane intersect)

Solving to lambda we get:

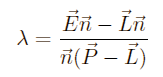
Now we enter lambda into the line formula from the beginning to get the shadow point P'

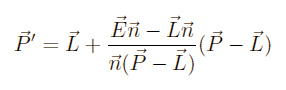
(P' is now the shadow-projected point. This means if P was a tiny sphere floating in space, and we would light it using our Light L, we would get a shadow at the Point P')

We now already have the correct projection, but we still need to turn this into a matrix. To do so, we split P' into the three coordinates. To make the notation somewhat easier we define:

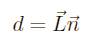and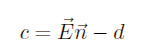

These two Variables make it easier now to read the formulas, they serve no other purpose. Now we use these two additional variables in our current formula:

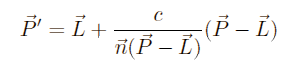
We can simplify this a bit more:

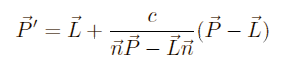
and

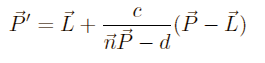
At this point, we can not calculate any further while keeping the vectors, so we split every vector into its x, y and z coordinate:

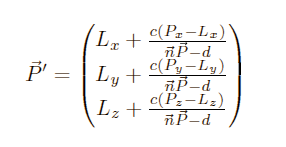
The scalar product can be written as:

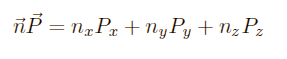
So we get

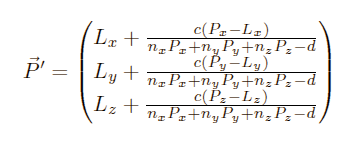
Bringing everything to the same denominator:

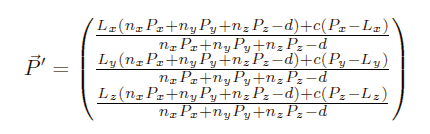
Extracting the braces:

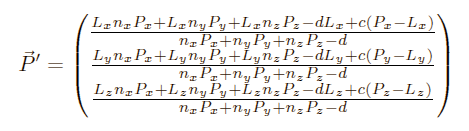
Combining for Px, Py and Pz

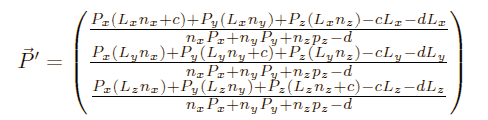
As you remember, a projection is calculated as shown:

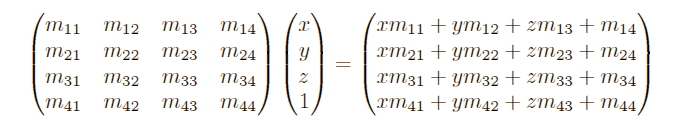
We need to find the corresponding values for the m-values that solve these equations:
(Left side is the matrix-multiplication-form, the right or own formula)

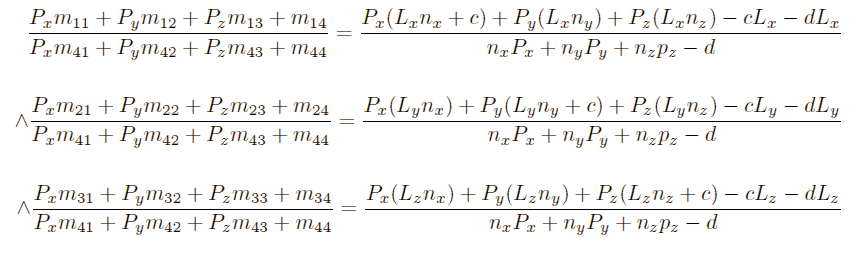
The solution you should get is:

I hope this article makes shadow projection somewhat clearer; okay this is really really basic stuff, but it was not this easy for me to figure out how to calculate the matrix and maybe there is someone out there who is happy to get one or two hints in the right direction.

Here you can finally see a screenshot of my example program running:

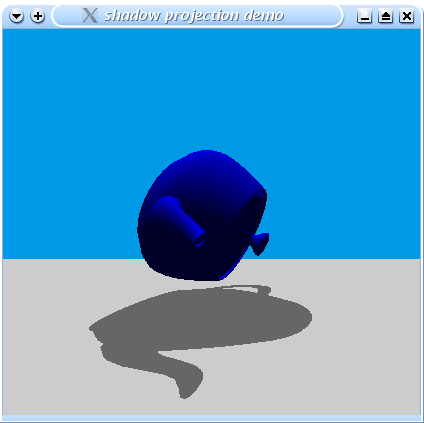Figure 2: My shadow projection example program

I invite you to download my example program here and to experiment a lot with it. Please note, that this program is written under and for Linux, but it may compile under Windows with a few adjustments.